Berücksichtigung von Durchläufern bei der Auswertung von Ermüdungsversuchen
- Ansprechperson:
- Förderung:
DFG
- Laufzeit:
2015 - 2017

Kurzbeschreibung
Die Voraussage der Lebensdauer einer häufig wiederholt beanspruchten Stahlschweißverbindung erfolgt zumeist mit Kerbfallkatalogen, die auf experimentell ermittelten Wöhlerkurven basieren. Die derzeit angewendeten Methoden zu deren Ermittlung, auf Basis von im Zeitfestigkeitsbereich durchgeführten Ermüdungsversuchen, erlauben es statistisch gesehen nicht, diese Kurven in den High Cycle Fatigue (HCF)-Bereich zu extrapolieren.
Zur rechnerischen Abschätzung der Lebensdauer eines Kerbdetails können verschiedene Methoden angewendet werden.
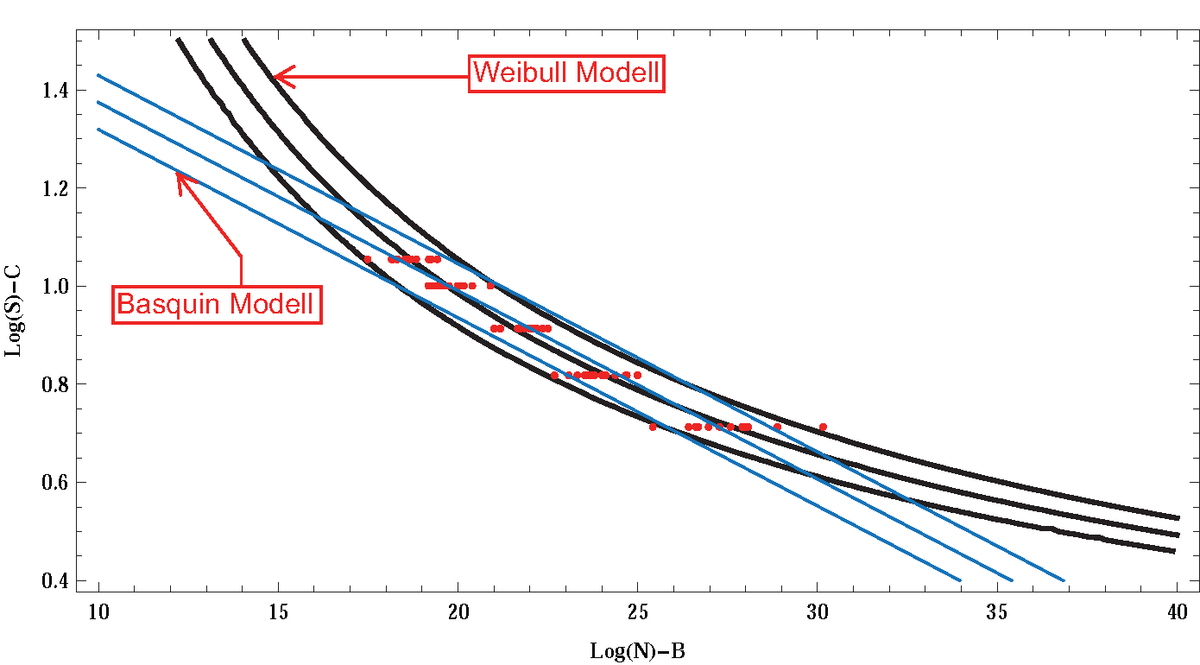
Eine Herangehensweise besteht in der statistischen Auswertung von Versuchsdaten durch eine vorgegebene Funktion (Wöhlerkurve), mit der die Bruchlastwechselzahlen in Abhängigkeit der aufgebrachten Spannungsschwingbreiten beschrieben werden.
Die Beschreibung einer Wöhlerkurve stellt wegen der stochastischen Natur des Ermüdungsvorgangs ein komplexes mathematisches Problem dar. Ausgehend von der Weibull-Verteilung, wird ein dimensionsloses Modell zur Beschreibung der Wöhlerkurven vorgeschlagen. Es gibt verschiedene mathematische Methoden zur Bestimmung der Parameter des Weibull-Modells, wobei diese Methoden hängen von den experimentellen Daten ab.
Ein Vorteil des Weibull-Modells ist neben der stochastischen Berücksichtigung von Durchläufern
die Möglichkeit, die Daten einer durchgelaufenen Probe bei der Wiederverwendung mit in die Auswertung einzubeziehen. Das bedeutet, eine nicht versagte Probe wird nach der Klassifikation als Durchläufer mit einer höheren Spannungsschwingbreite weiter untersucht.
Das Weibull Model ermöglicht eine allgemeine Darstellung der Wöhlerkurve und das Abschätzen der Vertrauensintervalle von Spannungsschwingbreite im HCF-Bereich.